XFGLENSES A Computer Program to visualize Gravitational Lenses
by Francisco Frutos Alfaro
The program xfglenses (Linux Version) needs the XForms, the Mesa Libraries (OpenGL) and the Image Library.
An old SGI version is also available: gllenses
Now, the source code is available xfglenses.zip
Paper
American Journal of Physics (February 2001 -- Volume 69, Issue 2, pp. 218-222)
ArXiv version of this paper.
JLenses
The Java version of XFGLenses, JLenses is now available. This new version was written by Hugo Solís Sánchez at the University of Costa Rica. A paper about it will appear soon. The source code is also available on request.
Keeton's Interface
An interface for Keeton's programs gravlens and lensmodel is almost ready. You also need XForms to run it.
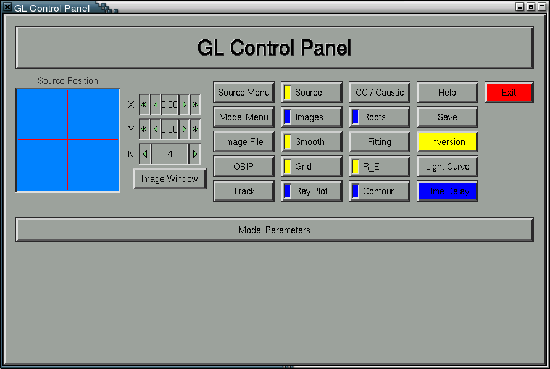
XFGLenses: The Control Panel
The Control Panel interface has the following items:
Model Menu (22 models, see below)
Source Menu (Filled Circle, Coloured Rings and Image File)
Source Positioner
Three counters, two for source positioning (X, Y) and one for adjusting the pixel resolution (N)
Buttons (Model Parameters, Image Window, Image File, OBIP, Track, Source, Images, Smooth, Grid, Ray Plot, CC / Caustic (not yet), Roots, Fitting (final phase), R_E, Contour, Help, Save, Inversion, Light Curve (not yet), Time Delay, Exit)
Sliders (if a model is chosen, then the corresponding sliders appears)
The user can click the Image Window button to see the visualization.
Model Menu
When this menu is clicked with the mouse, one gets a list of models. If one chooses one model, then the required sliders appear on the control panel. The model menu has the following models:
Chang Refsdal,
Double Plane Lens,
Transparent Sphere,
Singular Isothermal Sphere (SIS),
Nonsingular Isothermal Sphere (NIS),
Elliptical Model (SEF Book),
King Model,
Truncated King Model,
Hubble Model,
De Vaucouleur Model,
Spiral Model,
Multipole Lens,
Rotation Lens (Ibañez),
Uniform Ring (SEF Book),
Second Order Schwarzschild,
Elliptic SIS,
Elliptic NIS,
Elliptic King,
Elliptic Hubble,
Elliptic Plummer (not yet),
Kassiola-Kovner and,
Barkana
Source Menu
There are three sources:
Filled Circle
Coloured Rings
Image File
You can load any image using the File button.
Source Positioners
For positioning the source there are two possibilities:
Source Positioner and
Two counters (X, Y) for fine positioning
Input Fields
With the input fields one can position the observed images of a real gravitational lens. The images are then represented through circles. One can also try to fit it by means of parameter variations of a chosen model.
Buttons
Seventeen buttons are available:
Image Window : When clicking this button the Image Window appears.
Model Parameters : To disappear the sliders
Source : To visualize the source
Images : To visualize the images
Smooth : To smooth the lens images
Ray Plot : To show the Ray Plot
R_E : To dipect the Eintein Ring
Image File : To load an image File
OBIP : To show the observed image positions of the browser by means of circles
Save : To save the model images using gimp
Grid : To visualize the grid
Help
Exit
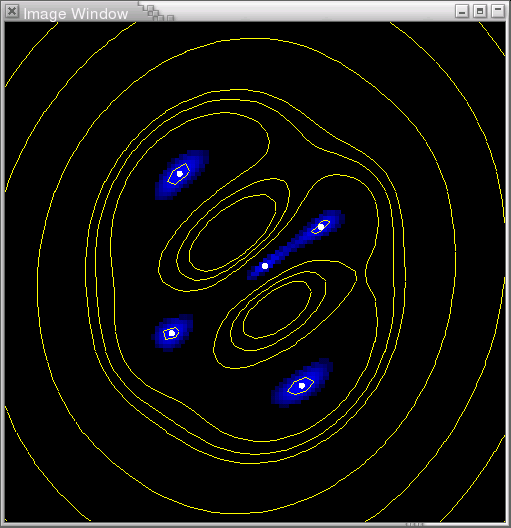
Image Window
On this window all events are interactively shown
OBIP
By cliking this button, the user get a window to enter the image positions and the number of images of the Lens System.
Add : To add an observed image position on the browser
Replace: To replace an observed image position on the browser
Remove : to remove an observed image position on the browser
Clear : To clear the observed image positions
Add : To draw concentric circles that represent the lens images
Browser : The information about the position of the images appears in it.
Sliders
The parameters of the chosen model are adjusted be means of these sliders. There are six sliders which all models have:
E : Length scale
Theta: To rotate (X, Y) coordinates
Gamma: Shear of the macrolens
Sigma: Constant surface mass density of the macrolens
Phi : Shear angle
R : Radius of the source
The Chang Refsdal Model
For this model there are no additional sliders.
The Double Plane Lens
This model has the following additional sliders:
m1 : Point mass in the first lens plane
m2 : Point mass in the second lens plane
Beta: distance between both lens planes
x1 : X position component of the mass m1
y1 : Y position component of the mass m1
x2 : X position component of the mass m2
y2 : Y position component of the mass m2
The Singular Isothermal Sphere
For this model there is only one additional slider:
Kappa: mass exponent
The Non Singular Isothermal Sphere
This model contains the following additional slider:
C : The core radius
Kappa: Constant central mass density
The Transparent Sphere
This model has the following additional slider:
C: The sphere radius
The Elliptical Model
For this model there are following additional sliders:
C : Core radius of the lens
Epsilon: Lens ellipticity
Alpha : Lens softness
Kappa : Constant central mass density
The Galactical Profiles
Following galactical model are available:
King Model
Truncated King Model
Hubble Model
De Vaucouleur Model
Spiralmodel
These models contain one additional slider (except the Truncated King Model):
Kappa: Constant central mass density
For the Truncated King Model there are two additional sliders:
C : The tidal radius of the lens
Kappa: Constant central mass density
Multipole Lens
For this model there are following additional sliders:
dx: X dipole moment component vector
dy: Y dipole moment component vector
q1: Component Q11 of the quadrupole moment tensor (Q11 + Q22 = 0)
q2: Component Q12 of the quadrupole moment tensor (Q12 = Q21)
Rotational Lens
This model has two additional sliders:
Sx: X angular momentum component
Sy: Y angular momentum component
The Uniform Ring
This model has three additional sliders:
Ri : The inner radius of the ring
Ro : The outer radius of the ring
Kappa: Constant surface mass density
Second Order Schwarschild
This model has one additional slider:
K: This parameter represents the term that appears in the GL equation if we consider the second order expansion of the Schwarzschild metric
Elliptic SIS
This model has two additional sliders:
Epsilon3: Lens ellipticity
Kappa : Constant surface mass density
Elliptic King
This model has three additional sliders:
C : Core radius of the lens
Epsilon2: Lens ellipticity
Kappa : Constant surface mass density
Elliptic Hubble
This model has three additional sliders:
C : Core radius of the lens
Epsilon2: Lens ellipticity
Kappa : Constant surface mass density
Elliptic NIS
This model has three additional sliders:
C : Core radius of the lens
Epsilon2: Lens ellipticity
Kappa : Constant surface mass density
Elliptic Plummer
This model has three additional sliders:
C : Core radius of the lens
Epsilon2: Lens ellipticity
Kappa : Constant surface mass density
The Kassiola Kovner Model
This model has four additional sliders:
C : Core radius of the lens
Kappa : Constant surface mass density
Q3 : Lens ellipticity
Thetai: Inclination angle
The Navarro Frenk White Model
This model has one additional sliders:
Kappa: Constant surface mass density
The Barkana Model
This model has four additional sliders:
C : Core radius of the lens
Kappa : Constant surface mass density
Epsilon2: Lens ellipticity
Alpha : Lens softness
Internet Subroutines
- Contouring: Translation from Fortran into C of Aramini's contouring program. We do not use his C version.
- Brent : Translation from Fortran into C of the program 554 of Netlib/Toms.
- Simplex: This algorithm is us
ed to optimize.
References
P. Schneider, J. Ehlers and E. E. Falco, Gravitational Lenses (SEF Book), Springer Verlag, 1992.
J. Huchra, Galactic Structure and Evolution, in R. Meyers, Encyclopedia of Astronomy and Astrophysics, 203-219, Academic Press, 1989.
J. Lawrence, Focusing of Gravitational Radiation by Interior Gravitational Fields, Nuovo Cimento, 6B, 225-235, 1971.
Coments and suggestions to: francisco.frutos@ucr.ac.cr or frutto@tat.physik.uni-tuebingen.de
Last version on 16 February 2008.